1111数学小考试卷

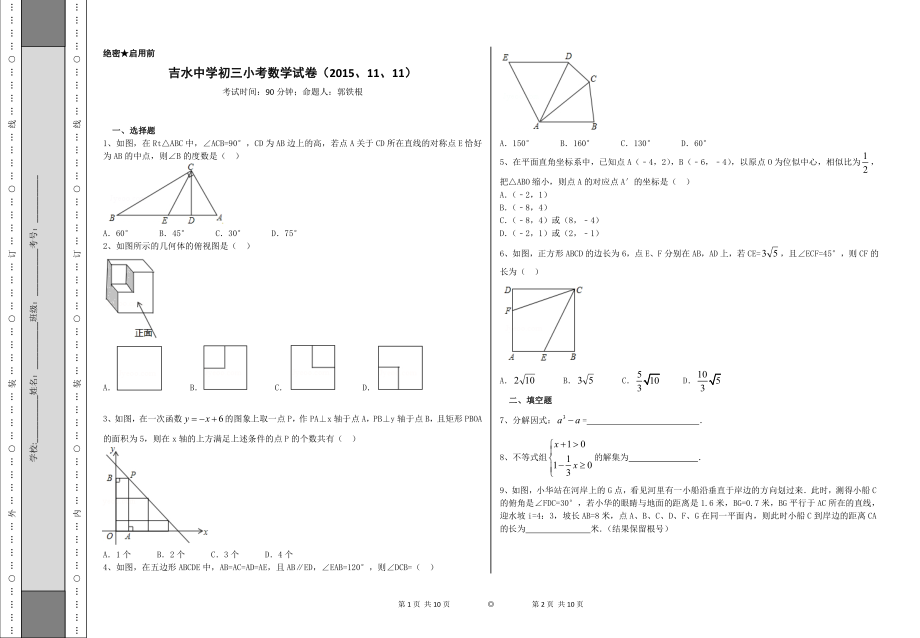
…………○…………内…………○…………装…………○…………订…………○…………线…………○…………学校:___________姓名：___________班级：___________考号：___________…………○…………外…………○…………装…………○…………订…………○…………线…………○…………绝密★启用前吉水中学初三小考数学试卷（2015、11、11）考试时间：90分钟；命题人：郭铁根一、选择题1、如图，在Rt△ABC中，∠ACB=90°，CD为AB边上的高，若点A关于CD所在直线的对称点E恰好为AB的中点，则∠B的度数是（ ） A．60° B．45° C．30° D．75°2、如图所示的几何体的俯视图是（ ）A． B． C． D．3、如图，在一次函数的图象上取一点P，作PA⊥x轴于点A，PB⊥y轴于点B，且矩形PBOA的面积为5，则在x轴的上方满足上述条件的点P的个数共有（ ）A．1个 B．2个 C．3个 D．4个4、如图，在五边形ABCDE中，AB=AC=AD=AE，且AB∥ED，∠EAB=120°，则∠DCB=（ ）A．150° B．160° C．130° D．60°5、在平面直角坐标系中，已知点A（﹣4，2），B（﹣6，﹣4），以原点O为位似中心，相似比为，把△ABO缩小，则点A的对应点A′的坐标是（ ）A．（﹣2，1） B．（﹣8，4）C．（﹣8，4）或（8，﹣4）D．（﹣2，1）或（2，﹣1）6、如图，正方形ABCD的边长为6，点E、F分别在AB，AD上，若CE=，且∠ECF=45°，则CF的长为（ ）A． B． C． D．二、填空题7、分解因式：= ．8、不等式组的解集为 ．9、如图，小华站在河岸上的G点，看见河里有一小船沿垂直于岸边的方向划过来．此时，测得小船C的俯角是∠FDC=30°，若小华的眼睛与地面的距离是1.6米，BG=0.7米，BG平行于AC所在的直线，迎水坡i=4：3，坡长AB=8米，点A、B、C、D、F、G在同一平面内，则此时小船C到岸边的距离CA的长为 米．（结果保留根号）10、下列四个命题中，正确的是 （填写正确命题的序号）①三角形的外心是三角形三边垂直平分线的交点；②函数与x轴只有一个交点，则；③半径分别为1和2的两圆相切，则两圆的圆心距为3；④若对于任意x＞1的实数，都有ax＞1成立，则a的取值范围是a≥1．11、如图，分别以Rt△ABC的直角边AC及斜边AB为边向外作等边△ACD、等边△ABE，EF⊥AB，垂足为F，连接DF，当= 时，四边形ADFE是平行四边形．12、如图，在直角坐标系xOy中，点A在第一象限，点B在x轴的正半轴上，△AOB为正三角形，射线OC⊥AB，在OC上依次截取点P1，P2，P3，…，Pn，使OP1=1，P1P2=3，P2P3=5，…，Pn﹣1Pn=2n﹣1（n为正整数），分别过点P1，P2，P3，…，Pn向射线OA作垂线段，垂足分别为点Q1，Q2，Q3，…，Qn，则点Qn的坐标为 ．13、抛物线（a，b，c为常数，且）经过点（﹣1，0）和（m，0），且1＜m＜2，当x＜﹣1时，y随着x的增大而减小．下列结论：①abc＞0；②a+b＞0；③若点A（﹣3，），点B（3，）都在抛物线上，则＜；④；⑤若c=-1，则b2—4ac<4a其中结论错误的是 ．（只填写序号）14、如图，抛物线y1=2x2向右平移2个单位，得抛物线y2,若P是抛物线y2对称轴上的一个动点，直线x=t平行于y轴，分别与直线y=x、抛物线y2交于点A、B．若△ABP是以点A或点B为直角顶点的等腰直角三角形，求满足条件的t的值，则t= ．三、解答题15、计算：． 16、在我市开展“五城联创”活动中，某工程队承担了某小区900米长的污水管道改造任务．工程队在改造完360米管道后，引进了新设备，每天的工作效率比原来提高了20%，结果共用27天完成了任务，问引进新设备前工程队每天改造管道多少米？17、如图，四边形ABCD为菱形，M为BC上一点，连接AM交对角线BD于点G，并且∠ABM=2∠BAM．（1）求证：AG=BG；（2）若点M为BC的中点，同时S△BMG=1，求三角形ADG的面积．18、希望学校九年级共有4个班，在世界地球日来临之际，每班各选拔10名学生参加环境知识竞赛，评出了一、二、三等奖各若干名，校学生会将获奖情况绘制成如图所示的两幅不完整的统计图，请依据图中信息解答下列问题：（1）本次竞赛获奖总人数为 人；获奖率为 ；（2）补全折线统计图；（3）已知获得一等奖的4人为每班各一人，学校采取随机抽签的方式在4人中选派2人参加上级团委组织的“爱护环境、保护地球”夏令营，请用列举法求出抽到的两人恰好来自二、三班的概率．19、如图，直线和相交于点A，且分别与x轴交于B，C两点，过点A的双曲线（）与直线的另一交点为点D．（1）求双曲线的解析式；（2）求△BCD的面积．20、大华服装厂生产一件秋冬季外套需面料1.2米，里料0.8米，已知面料的单价比里料的单价的2倍还多10元，一件外套的布料成本为76元．（1）求面料和里料的单价；（2）该款外套9月份投放市场的批发价为150元/件，出现购销两旺态势，10月份进入批发淡季，厂方决定采取打折促销．已知生产一件外套需人工等固定费用14元，为确保每件外套的利润不低于30元．①设10月份厂方的打折数为m，求m的最小值；（利润=销售价﹣布料成本﹣固定费用）②进入11月份以后，销售情况出现好转，厂方决定对VIP客户在10月份最低折扣价的基础上实施更大的优惠，对普通客户在10月份最低折扣价的基础上实施价格上浮．已知对VIP客户的降价率和对普通客户的提价率相等，结果一个VIP客户用9120元批发外套的件数和一个普通客户用10080元批发外套的件数相同，求VIP客户享受的降价率．21、已知关于x的一元二次方程．（1）若方程有实数根，求实数的取值范围；（2）若方程两实数根分别为，，且满足，求实数的值22、如图，已知抛物线（）与x轴交于点A（1，0）和点B（﹣3，0），与y轴交于点C，且OC=OB．（1）求此抛物线的解析式；（2）若点E为第二象限抛物线上一动点，连接BE，CE，求四边形BOCE面积的最大值，并求出此时点E的坐标；（3）点P在抛物线的对称轴上，若线段PA绕点P逆时针旋转90°后，点A的对应点A′恰好也落在此抛物线上，求点P的坐标．34．（6分）化简：．35．（6分）如图，CA=CD，∠B=∠E，∠BCE=∠ACD．求证：AB=DE．37．（9分）端午节是我国的传统节日，人们有吃粽子的习惯．某校数学兴趣小组为了了解本校学生喜爱粽子的情况，随机抽取了50名同学进行问卷调查，经过统计后绘制了两幅尚不完整的统计图（注：每一位同学在任何一种分类统计中只有一种选择）请根据统计图完成下列问题：（1）扇形统计图中，“很喜欢”所对应的圆心角为 度；条形统计图中，喜欢“糖馅”粽子的人数为 人；（2）若该校学生人数为800人，请根据上述调查结果，估计该校学生中“很喜欢”和“比较喜欢”粽子的人数之和；（3）小军最爱吃肉馅粽子，小丽最爱吃糖馅粽子．某天小霞带了重量、外包装完全一样的肉馅、糖馅、枣馅、海鲜馅四种粽子各一只，让小军、小丽每人各选一只．请用树状图或列表法求小军、小丽两人中有且只有一人选中自己最爱吃的粽子的概率．．39．（8分）如图，点A（，）在双曲线（）上．（1）求k的值；（2）在y轴上取点B（0，1），为双曲线上是否存在点D，使得以AB，AD为邻边的平行四边形ABCD的顶点C在x轴的负半轴上？若存在，求出点D的坐标；若不存在，请说明理由．40．（8分）为支持国家南水北调工程建设，小王家由原来养殖户变为种植户，经市场调查得知，种植草莓不超过20亩时，所得利润y（元）与种植面积m（亩）满足关系式y=1500m；超过20亩时，y=1380m+2400．而当种植樱桃的面积不超过15亩时，每亩可获得利润1800元；超过15亩时，每亩获得利润z（元）与种植面积x（亩）之间的函数关系如下表（为所学过的一次函数、反比例函数或二次函数中的一种）．（1）设小王家种植x亩樱桃所获得的利润为P元，直接写出P关于x的函数关系式，并写出自变量的取值范围；（2）如果小王家计划承包40亩荒山种植草莓和樱桃，当种植樱桃面积x（亩）满足0＜x＜20时，求小王家总共获得的利润w（元）的最大值．42．（12分）已知抛物线C1：（）经过点A（﹣1，0）和B（3，0）．（1）求抛物线C1的解析式，并写出其顶点C的坐标；（2）如图1，把抛物线C1沿着直线AC方向平移到某处时得到抛物线C2，此时点A，C分别平移到点D，E处．设点F在抛物线C1上且在x轴的下方，若△DEF是以EF为底的等腰直角三角形，求点F的坐标；（3）如图2，在（2）的条件下，设点M是线段BC上一动点，EN⊥EM交直线BF于点N，点P为线段MN的中点，当点M从点B向点C运动时：①tan∠ENM的值如何变化？请说明理由；②点M到达点C时，直接写出点P经过的路线长．第9页 共10页 ◎ 第10页 共10页本卷由系统自动生成，请仔细校对后使用，答案仅供参考。

参考答案1．A．【解析】试题分析：∵直线AB∥CD，∠BNE=30°，∴∠DME=∠BNE=30°．∵MG是∠EMD的角平分线，∴∠EMG=∠EMD=15°．故选A．考点：平行线的性质．2．B．【解析】试题分析：根据图示，可得商品的外包装盒是底面直径是10cm，高是20cm的圆柱，∴这个包装盒的体积是：（cm3）．故选B．考点：由三视图判断几何体．3．C．【解析】试题分析：如图1，所示：函数图象没有交点．如图2所示：函数图象有1个交点．如图3所示函数图象有3个交点．如图4所示，图象有两个交点．如图5所示；函数图象有一个交点．综上所述，共有4中情况．故选C．考点：二次函数图象与几何变换．4．C．【解析】试题分析：∵在Rt△ABC中，∠ACB=90°，CD为AB边上的高，点A关于CD所在直线的对称点E恰好为AB的中点，∴∠CED=∠A，CE=BE=AE，∴∠ECA=∠A，∠B=∠BCE，∴△ACE是等边三角形，∴∠CED=60°，∴∠B=∠CED=30°．故选C．考点：1．直角三角形斜边上的中线；2．轴对称的性质．5．C．【解析】试题分析：①当0＜x＜6时，设点P（x，﹣x+6），∴矩形PBOA的面积为5，∴x（﹣x+6）=5，化简，解得，，∴P1（1，5），P2（5，1），②当x＜0时，设点P（x，﹣x+6），∴矩形PBOA的面积为5，∴﹣x（﹣x+6）=5，化简，解得，（舍去），∴P3（，），∴在x轴的上方满足上述条件的点P的个数共有3个．故选C．考点：1．一次函数图象上点的坐标特征；2．分类讨论．6．A．【解析】试题分析：∵AB∥ED，∴∠E=180°﹣∠EAB=180°﹣120°=60°，∵AD=AE，∴△ADE是等边三角形，∴∠EAD=60°，∴∠BAD=∠EAB﹣∠DAE=120°﹣60°=60°，∵AB=AC=AD，∴∠B=∠ACB，∠ACD=∠ADC，在四边形ABCD中，∠BCD=（360°﹣∠BAD）=（360°﹣60°）=150°．故选A．考点：1．等腰三角形的性质；2．平行线的性质；3．多边形内角与外角．7．B．【解析】试题分析：因为，，当时，可得：，则，则y的最小值为1；当时，可得：，则，则y＜1，故选B．考点：1．一次函数的性质；2．新定义；3．分类讨论．8．B．【解析】试题分析：由题意得，x﹣1≥0，解得x≥1．故选B．考点：函数自变量的取值范围．9．D．【解析】试题分析：从上面看是一个大正方形，大正方形内部的左下角是一个小正方形，故选D．考点：简单组合体的三视图．10．D．【解析】试题分析：∵点A（﹣4，2），B（﹣6，﹣4），以原点O为位似中心，相似比为，把△ABO缩小，∴点A的对应点A′的坐标是：（﹣2，1）或（2，﹣1）．故选D．考点：1．位似变换；2．坐标与图形性质．11．A．【解析】试题分析：∵当x=1时，的值为﹣2，∴，∴，∴=（﹣3﹣1）×（1+3）=﹣16．故选A．考点：整式的混合运算—化简求值．12．B．【解析】试题分析：一只蚂蚁从O点出发，沿着扇形OAB的边缘匀速爬行，在开始时经过半径OA这一段，蚂蚁到O点的距离随运动时间t的增大而增大；到弧AB这一段，蚂蚁到O点的距离S不变，图象是与x轴平行的线段；走另一条半径OB时，S随t的增大而减小；故选B．考点：1．动点问题的函数图象；2．分段函数．13．D．【解析】试题分析：设连续搭建三角形x个，连续搭建正六边形y个．由题意得，，解得：．故选D．考点：规律型：图形的变化类．14．A．【解析】试题分析：如图，延长FD到G，使DG=BE，连接CG、EF；∵四边形ABCD为正方形，在△BCE与△DCG中，∵CB=CD，∠CBE=∠CDG，BE=DG，∴△BCE≌△DCG（SAS），∴CG=CE，∠DCG=∠BCE，∴∠GCF=45°，在△GCF与△ECF中，∵GC=EC，∠GCF=∠ECF，CF=CF，∴△GCF≌△ECF（SAS），∴GF=EF，∵CE=，CB=6，∴BE===3，∴AE=3，设AF=x，则DF=6﹣x，GF=3+（6﹣x）=9﹣x，∴EF==，∴，∴x=4，即AF=4，∴GF=5，∴DF=2，∴CF===，故选A．考点：1．全等三角形的判定与性质；2．勾股定理；3．正方形的性质；4．综合题；5．压轴题．15．．【解析】试题分析：==．故答案为：．考点：1．提公因式法与公式法的综合运用；2．因式分解．16．﹣1＜x≤3．【解析】试题分析： ，由①得x＞﹣1，由②得x≤3．故原不等式组的解集为﹣1＜x≤3．故答案为：﹣1＜x≤3．考点：解一元一次不等式组．17．甲．【解析】试题分析：∵=（6+7+6+8+8）=7，=（5+7+8+8+7）=7；∴S2甲= [（6﹣7）2+（7﹣7）2+（6﹣7）2+（8﹣7）2+（8﹣7）2=，S2乙= [（5﹣7）2+（7﹣7）2+（8﹣7）2+（8﹣7）2+（7﹣7）2=；∴S2甲＜S2乙，∴甲在射击中成绩发挥比较稳定．故答案为：甲．考点：1．方差；2．条形统计图．18．（，）．【解析】试题分析：∵△AOB为正三角形，射线OC⊥AB，∴∠AOC=30°，又∵Pn﹣1Pn=2n﹣1，PnQn⊥OA，∴OQn=（OP1+P1P2+P2P3+…+Pn﹣1Pn）=（1+3+5+…+2n﹣1）=，∴Qn的坐标为（cos60°，sin60°），∴Qn的坐标为（，）．故答案为：（，）．考点：1．相似三角形的判定与性质；2．坐标与图形性质；3．规律型．19．①④．【解析】试题分析：三角形的外心是三角形三边垂直平分线的交点，所以①正确；函数与x轴只有一个交点，则或1，所以②错误；半径分别为1和2的两圆相切，则两圆的圆心距为1或3；若对于任意x＞1的实数，都有ax＞1成立，则a的取值范围是a≥1，所以④正确．故答案为：①④．考点：命题与定理．20．3.0×105．【解析】试题分析：将300000用科学记数法表示为3.0×105．故答案为：3.0×105．考点：科学记数法—表示较大的数．21．﹣1，0．【解析】试题分析：，解①得：x≥﹣1，解②得：x＜1，则不等式组的解集是：﹣1≤x＜1，则整数解是：﹣1，0．故答案为：﹣1，0．考点：一元一次不等式组的整数解．22．．【解析】试题分析：当=时，四边形ADFE是平行四边形．理由如下：∵=，∴∠CAB=30°，∵△ABE为等边三角形，EF⊥AB，∴EF为∠BEA的平分线，∠AEB=60°，AE=AB，∴∠FEA=30°，又∠BAC=30°，∴∠FEA=∠BAC，在△ABC和△EAF中，∵∠ACB=∠EFA，∠BAC=∠AEF，AB=AE，∴△ABC≌△EAF（AAS），∵∠BAC=30°，∠DAC=60°，∴∠DAB=90°，即DA⊥AB，∵EF⊥AB，∴AD∥EF，∵△ABC≌△EAF，∴EF=AC=AD，∴四边形ADFE是平行四边形．故答案为：．考点：1．平行四边形的判定；2．等边三角形的性质；3．综合题；4．压轴题．23．．【解析】试题分析：过点B作BE⊥AC于点E，延长DG交CA于点H，得Rt△ABE和矩形BEHG．∵i=，AB=8米，∴BE=，AE=，∵DG=1.6，BG=0.7，∴DH=DG+GH=1.6+=8，AH=AE+EH=+0.7=5.5，在Rt△CDH中，∵∠C=∠FDC=30°，DH=8，tan30°=，∴CH=，又∵CH=CA+5.5，即=CA+5.5，∴CA=（米）．故答案为：．考点：1．解直角三角形的应用-仰角俯角问题；2．解直角三角形的应用-坡度坡角问题；3．综合题．24．③⑤．【解析】试题分析：如图，∵抛物线开口向上，∴a＞0，∵抛物线的对称轴在y轴的右侧，∴b＜0，∵抛物线与y轴的交点在x轴上方，∴c＜0，∴abc＞0，所以①的结论正确；∵抛物线过点（﹣1，0）和（m，0），且1＜m＜2，∴0＜＜，∴a+b＞0，所以②的结论正确；∵点A（﹣3，）到对称轴的距离比点B（3，）到对称轴的距离远，∴＞，所以③的结论错误；∵抛物线过点（﹣1，0），（m，0），∴a﹣b+c=0，，∴，，∴，所以④的结论正确；∵，而，∴，∴，所以⑤的结论错误．故答案为：③⑤．考点：1．二次函数图象与系数的关系；2．数形结合；3．综合题．25．（1）2x2﹣8x+8；（2）1或3或．【解析】试题分析：（1）抛物线y1=2x2向右平移2个单位，得：y=2（x﹣2）2=2x2﹣8x+8；故抛物线y2的解析式为y2=2x2﹣8x+8．（2）由（1）知：抛物线y2的对称轴为x=2，故P点横坐标为2；当x=t时，直线y=x=t，故A（t，t）；则y2=2x2﹣8x+8=2t2﹣8t+8，故B（t，2t2﹣8t+8）；若△ABP是以点A或点B为直角顶点的等腰直角三角形，则有AB=AP或AB=BP，此时AB=|2t2﹣8t+8﹣t|，AP=|t﹣2|，可得：|t﹣2|=|2t2﹣8t+8﹣t|；当2t2﹣8t+8﹣t=t﹣2时，如图1，t2﹣5t+5=0，解得t1=；当2t2﹣8t+8﹣t=2﹣t时，如图2，t2﹣4t+3=0，解得t2=1，t3=3；故符合条件的t值为：1或3或．考点：二次函数综合题．26．2．【解析】试题分析：分别利用特殊角的三角函数值、绝对值的性质、负整数指数幂的计算法则分别计算出各数，再进行实数混合运算计算即可；试题解析：原式===2．考点：1．实数的运算；2．负整数指数幂；3．特殊角的三角函数值．27．1．【解析】试题分析：原式==1，故答案为：1．考点：1．实数的运算；2．零指数幂；3．负整数指数幂．28．（1）证明见试题解析；（2）4．【解析】试题分析：（1）由菱形的对角线平分一组对角，得出∠ABD=∠CBD，再由∠ABM=2∠BAM，得出∠ABD=∠BAM，即可得出结论．（2）由相似三角形面积的比等于相似比的平方即可求得．试题解析：（1）∵四边形ABCD是菱形，∴∠ABD=∠CBD，∵∠ABM=2∠BAM，∴∠ABD=∠BAM，∴AG=BG；（2）∵AD∥BC，∴△ADG∽△MBG，∴，∵点M为BC的中点，∴=2，∴=4，∵S△BMG=1，∴S△ADG=4．考点：菱形的性质．29．（1）20；50%；（2）作图见试题解析；（3）．【解析】试题分析：（1）先利用扇形统计图计算出一等奖所占的百分比，然后用获奖总人数=一等奖的人数÷它所占百分比，再计算获奖率；（2）分别计算出二、三等奖的人数，然后补全折线统计图；（3）利用树状图法列举出所有的可能，进而利用概率公式求出即可．试题解析：（1）本次竞赛获奖总人数=4÷=20（人），获奖率=×100%=50%；故答案为：20；50%；（2）三等奖的人数=20×50%=10（人），二等奖的人数=20﹣4﹣10=6（人），折线统计图为：（3）画树状图为：共有12种等可能的结果数，其中抽到的两人恰好来自二、三班的有2种情况，所以抽到的两人恰好来自二、三班的概率==．考点：1．列表法与树状图法；2．扇形统计图；3．折线统计图．30．（1）；（2）2．【解析】试题分析：（1）解方程组，得A（1，2），然后把A（1，2）代入中求出k的值即可得到反比例函数解析式；（2）解方程组，得D（2，1），再利用x轴上点的坐标特征确定B点和C点坐标，由三角形面积公式求解即可．试题解析：（1）解方程组，得：，则A（1，2），把A（1，2）代入得k=1×2=2，所以反比例函数解析式为；（2）解方程组，得或，则D（2，1），当y=0时，x+1=0，解得x=﹣1，则B（﹣1，0）；当y=0时，﹣x+3=0，解得x=3，则C（3，0），所以△BCD的面积=×（3+1）×1=2．考点：反比例函数与一次函数的交点问题．31．（1）面料的单价为50元/米，里料的单价为20元/米；（2）①8；②5%．【解析】试题分析：（1）设里料的单价为x元/米，面料的单价为（2x+10）元/米，根据题意列方程求解即可；（2）①设打折数为m，根据题意列不等式求解即可；②设vip客户享受的降价率为x，然后根据VIP客户与普通用户批发件数相同列方程求解即可．试题解析：（1）设里料的单价为x元/米，面料的单价为（2x+10）元/米．根据题意得：0.8x+1.2（2x+10）=76．解得：x=20.2x+10=2×20+10=50．答：面料的单价为50元/米，里料的单价为20元/米；（2）①设打折数为m．根据题意得：150×﹣76﹣14≥30．解得：m≥8．∴m的最小值为8．答：m的最小值为8；②150×0.8=120元．设vip客户享受的降价率为x．根据题意得：，解得：x=0.05，经检验x=0.05是原方程的解．答：vip客户享受的降价率为5%．考点：1．分式方程的应用；2．一元一次方程的应用；3．一元一次不等式的应用．32．（1）证明见试题解析；（2）BE+CF的值是定值，为等边△ABC边长的一半．【解析】试题分析：（1）连结OB、OD，如图1，由于D为BC的中点，由垂径定理的推理得OD⊥BC，∠BOD=∠COD，即可得到∠BOD=∠M=60°，则∠OBD=30°，所以∠ABO=90°，于是得到AB是⊙O的切线；（2）作DM⊥AB于M，DN⊥AC于N，连结AD，如图2，由△ABC为正三角形，D为BC的中点，得到AD平分∠BAC，∠BAC=60°，利用角平分线性质得DM=DN，得∠MDN=120°，由∠EDF=120°，得到∠MDE=∠NDF，于是有△DME≌△DNF，得到ME=NF，得到BE+CF=BM+CN，由BM=BD，CN=OC，得到BE+CF=BC，即可判断BE+CF的值是定值，为等边△ABC边长的一半．试题解析：（1）连结OB、OD，如图1，∵D为BC的中点，∴OD⊥BC，∠BOD=∠COD，∴∠ODB=90°，∵∠BMC=∠BOC，∴∠BOD=∠M=60°，∴∠OBD=30°，∵△ABC为正三角形，∴∠ABC=60°，∴∠ABO=60°+30°=90°，∴AB⊥OB，∴AB是⊙O的切线；（2）BE+CF的值是为定值．作DM⊥AB于M，DN⊥AC于N，连结AD，如图2，∵△ABC为正三角形，D为BC的中点，∴AD平分∠BAC，∠BAC=60°，∴DM=DN，∠MDN=120°，∵∠EDF=120°，∴∠MDE=∠NDF，在△DME和△DNF中，∵∠DME=∠DNF．DM=DN，∠MDE=∠NDF，∴△DME≌△DNF，∴ME=NF，∴BE+CF=BM﹣EM+CN+NF=BM+CN，在Rt△DMB中，∵∠DBM=60°，∴BM=BD，同理可得CN=OC，∴BE+CF=OB+OC=BC，∴BE+CF的值是定值，为等边△ABC边长的一半．考点：1．切线的判定；2．等边三角形的性质；3．定值问题；4．探究型；5．综合题；6．压轴题．33．（1）；（2）当a=时，S四边形BOCE最大，且最大值为，此时，点E坐标为（，）；（3）P（﹣1，1）或（﹣1，﹣2）．【解析】试题分析：（1）将A、B两点的坐标代入抛物线的解析式中，即可求出二次函数的解析式；（2）过E作EF⊥x轴于F．设E（a，）（﹣3＜a＜0），则EF=，BF=a+3，OF=﹣a，∴S四边形BOCE==BF•EF+（OC+EF）•OF =，配方即可得出结论，当a=时，=大，即可得到点E的坐标；（3）由P在抛物线的对称轴上，设出P坐标为（﹣2，m），如图所示，过A′作A′N⊥对称轴于N，由旋转的性质可证明△A′NP≌△PMA，得到A′N=PM=|m|，PN=AM=2，表示出A′坐标，将A′坐标代入抛物线解析式中求出相应m的值，即可确定出P的坐标．试题解析：（1）∵抛物线（）与x轴交于点A（1，0）和点B（﹣3，0），∴OB=3，∵OC=OB，∴OC=3，∴c=3，∴，解得：，∴所求抛物线解析式为：；（2）如图2，过点E作EF⊥x轴于点F，设E（a，）（﹣3＜a＜0），∴EF=，BF=a+3，OF=﹣a，∴S四边形BOCE==BF•EF+（OC+EF）•OF===，∴当a=时，S四边形BOCE最大，且最大值为．此时，点E坐标为（，）；（3）∵抛物线的对称轴为x=﹣1，点P在抛物线的对称轴上，∴设P（﹣1，m），∵线段PA绕点P逆时针旋转90°后，点A的对应点A′恰好也落在此抛物线上，如图，∴PA=PA′，∠APA′=90°，如图3，过A′作A′N⊥对称轴于N，设对称轴于x轴交于点M，∴∠NPA′+∠MPA=∠NA′P+∠NPA′=90°，∴∠NA′P=∠NPA，在△A′NP与△APM中，∵∠A′NP=∠AMP=90°，∠NA′P=∠MPA，PA′=AP，∴△A′NP≌△PMA，∴A′N=PM=|m|，PN=AM=2，∴A′（m﹣1，m+2），代入得：，解得：m=1，m=﹣2，∴P（﹣1，1），（﹣1，﹣2）．考点：1．二次函数综合题；2．二次函数的最值；3．最值问题；4．旋转的性质；5．综合题；6．压轴题．34．．【解析】试题分析：括号中两项通分后利用同分母分式的加减法则计算，同时利用除法法则变形，约分即可得到结果．试题解析：原式===．考点：分式的混合运算．35．证明见试题解析．【解析】试题分析：由∠BCE=∠ACD，得到∠ACB=∠DCE，从而得到△ABC≌△DEC，即可得到结论．试题解析：∵∠BCE=∠ACD，∴∠ACB=∠DCE，在△ABC与△DEC中，∵∠ACB=∠DCE，∠B=∠E，CA=CD，∴△ABC≌△DEC（AAS），∴AB=DE．考点：全等三角形的判定与性质．36．36．【解析】试题分析：设原来每天改造管道x米，则引进新设备前工程队每天改造管道（1+20%）x米，根据题中等量关系列出方程，解方程即可．试题解析：设原来每天改造管道x米，由题意得：，解得：x=30，经检验：x=30是原分式方程的解，（1+20%）x=1.2×30=36．答：引进新设备前工程队每天改造管道36米．考点：分式方程的应用．37．（1）144，3；（2）600；（3）．【解析】试题分析：（1）用360°乘以很喜欢所占的百分比即可求得其圆心角，直接从条形统计图中得到喜欢糖馅的人数即可；（2）用总人数800乘以所对应的百分比即可；（3）画出树状图，然后利用概率公式即可求解．试题解析：（1）扇形统计图中，“很喜欢”所对应的圆心角为360°×40%=144度；条形统计图中，喜欢“糖馅”粽子的人数为 3人；（2）学生有800人，估计该校学生中“很喜欢”和“比较喜欢”粽子的人数之和为800×（1﹣25%）=600（人）；（3）肉馅、糖馅、枣馅、海鲜馅四种粽子分别用A、B、C、D表示，画图如下：∵共12种等可能的结果，其中小军、小丽两人中有且只有一人选中自己最爱吃的粽子有4种，∴P（小军、小丽两人中有且只有一人选中自己最爱吃的粽子）==．考点：1．列表法与树状图法；2．用样本估计总体；3．扇形统计图；4．条形统计图．38．（1）；（2）2．【解析】试题分析：（1）若方程有实数根，则△≥0，解不等式即可；（2）由根与系数的关系得到，，由和，得到，即，代入即可得到结果．试题解析：（1）∵关于x的一元二次方程有实数根，∴△≥0，即，∴；（2）根据题意得，，∵，∴，∵，∴，∴，即，解得m=2，m=﹣14（舍去），∴m=2．考点：1．根的判别式；2．根与系数的关系；3．综合题．39．（1）﹣4；（2）D（，）．【解析】试题分析：（1）把A的坐标代入反比例函数即可得出结论；（2）由平行四边形的性质得出D点纵坐标，进而代入函数解析式得出D点横坐标即可．试题解析：（1）∵点A（，）在双曲线（）上，∴k=（）（）=1﹣5=﹣4；（2）过点A作AE⊥y轴于点E，过点D作DF⊥x轴于点F，∵四边形ABCD是以AB，AD为邻边的平行四边形ABCD，∴DCAB，∵A A（，），B（0，1），∴BE=，由题意可得：DF=BE=，则，解得：x=，∴点D的坐标为：（，）．考点：1．反比例函数综合题；2．存在型．40．（1）；（2）61500元．【解析】试题分析：（1）根据图表的性质，可以得出P关于x的函数关系式和出x的取值范围．（2）根据利润=亩数×每亩利润，可得①当0＜x≤15时， ②当15＜x＜20时，利润的函数式，利用二次函数的性质即可解题；试题解析：（1）观察图表的数量关系，可以得出P关于x的函数关系式为：；（2）∵利润=亩数×每亩利润，∴①当0＜x≤15时，W=1800x+1380（40﹣x）+2400=420x+55200，当x=15时，W有最大值，W最大=6300+55200=61500；②当15＜x＜20，W=﹣20x+2100+1380（40﹣x）+2400=﹣1400x+59700，∵﹣1400x+59700＜61500，∴x=15时有最大值为：61500元．综上所述：当x=15时，W有最大值，W最大=61500．考点：1．二次函数的应用；2．二次函数的最值；3．最值问题；4．分段函数；5．综合题．41．（1）证明见试题解析；（2）；（3）3．【解析】试题分析：（1）连结OD，如图1，由已知得到∠BAD=∠CAD，得到，再由垂径定理得OD⊥BC，由于BC∥EF，则OD⊥DF，于是可得结论；（2）连结OB，OD交BC于P，作BH⊥DF于H，如图1，先证明△OBD为等边三角形得到∠ODB=60°，OB=BD=，得到∠BDF=∠DBP=30°，在Rt△DBP中得到PD=，PB=3，在Rt△DEP中利用勾股定理可算出PE=2，由于OP⊥BC，则BP=CP=3，得到CE=1，由△BDE∽△ACE，得到AE的长，再证明△ABE∽△AFD，可得DF=12，最后利用S阴影部分=S△BDF﹣S弓形BD=S△BDF﹣（S扇形BOD﹣S△BOD）进行计算；（3）连结CD，如图2，由可设AB=4x，AC=3x，设BF=y，由得到CD=BD=，由△BFD∽△CDA，得到xy=4，再由△FDB∽△FAD，得到16﹣4y=xy，则16﹣4y=4，然后解方程即可得到BF=3．试题解析：（1）连结OD，如图1，∵AD平分∠BAC交⊙O于D，∴∠BAD=∠CAD，∴，∴OD⊥BC，∵BC∥EF，∴OD⊥DF，∴DF为⊙O的切线；（2）连结OB，连结OD交BC于P，作BH⊥DF于H，如图1，∵∠BAC=60°，AD平分∠BAC，∴∠BAD=30°，∴∠BOD=2∠BAD=60°，∴△OBD为等边三角形，∴∠ODB=60°，OB=BD=，∴∠BDF=30°，∵BC∥DF，∴∠DBP=30°，在Rt△DBP中，PD=BD=，PB=PD=3，在Rt△DEP中，∵PD=，DE=，∴PE==2，∵OP⊥BC，∴BP=CP=3，∴CE=3﹣2=1，易证得△BDE∽△ACE，∴AE：BE=CE：DE，即AE：5=1：，∴AE=，∵BE∥DF，∴△ABE∽△AFD，∴，即，解得DF=12，在Rt△BDH中，BH=BD=，∴S阴影部分=S△BDF﹣S弓形BD=S△BDF﹣（S扇形BOD﹣S△BOD）==；（3）连结CD，如图2，由可设AB=4x，AC=3x，设BF=y，∵，∴CD=BD=，∵∠F=∠ABC=∠ADC，∵∠FDB=∠DBC=∠DAC，∴△BFD∽△CDA，∴，即，∴xy=4，∵∠FDB=∠DBC=∠DAC=∠FAD，而∠DFB=∠AFD，∴△FDB∽△FAD，∴，即，整理得16﹣4y=xy，∴16﹣4y=4，解得y=3，即BF的长为3．考点：1．圆的综合题；2．相似三角形的判定与性质；3．切线的判定与性质；4．综合题；5．压轴题．42．（1），顶点C（1，2）；（2）F（﹣3，﹣6）；（3）①tan∠ENM=2，是定值，不发生变化；②．【解析】试题分析：（1）把A、B两点的坐标代入即可求得解析式，把解析式化成顶点式即可求得顶点坐标；（2）由A、C的坐标求得直线AC的解析式，由题意求得EF=4，由EF∥y轴，设F（m，），则E（m，m+1），从而得出，解方程即可求得F的坐标；（3）①由DF⊥AC，BC⊥AC，得到DC∥BC，由DF=BC=AC，得到四边形DFBC是矩形，作EG⊥AC，交BF于G，得到△EGN∽△EMC，得到tan∠ENM==2，故tan∠ENM的值为定值，不发生变化；②由勾股定理和三角形相似得到EN=，由三角形中位线定理即可得出结果．试题解析：（1）∵抛物线C1：（）经过点A（﹣1，0）和B（3，0），∴解得：，∴抛物线C1的解析式为，∵=，∴顶点C的坐标为（1，2）；（2）如图1，作CH⊥x轴于H，∵A（﹣1，0），C（1，2），∴AH=CH=2，∴∠CAB=∠ACH=45°，∴直线AC的解析式为，∵△DEF是以EF为底的等腰直角三角形，∴∠DEF=45°，∴∠DEF=∠ACH，∴EF∥y轴，∵DE=AC=，∴EF=4，设F（m，），则E（m，m+1），∴，解得m=±3，∴F（﹣3，﹣6）；（3）①tan∠ENM的值为定值，不发生变化．理由如下：如图2，∵DF⊥AC，BC⊥AC，∴DC∥BC，∵DF=BC=AC，∴四边形DFBC是矩形，作EG⊥AC，交BF于G，∴EG=BC=AC=，∵EN⊥EM，∴∠MEN=90°，∵∠CEG=90°，∴∠CEM=∠NEG，∴△EGN∽△EMC，∴，∵F（﹣3，﹣6），EF=4，∴E（﹣3，﹣2），∵C（1，2），∴EC==，∴==2，∴tan∠ENM==2，∴tan∠ENM的值为定值，不发生变化；②点P经过的路径是线段P1P2，如图3，∵四边形BCEG是矩形，GP2=CP2，∴EP2=BP2，∵△EGN∽△ECB，∴，∵EC=，EG=BC=，∴EB=，∴，∴EN=，∵P1P2是△BEN的中位线，∴P1P2=EN=；∴点M到达点C时，点P经过的路线长为．考点：1．二次函数综合题；2．动点型；3．定值问题；4．综合题；5．压轴题．答案第17页，总18页。