中考数学总复习 第六章 圆 第21讲 圆的基本性质试题1

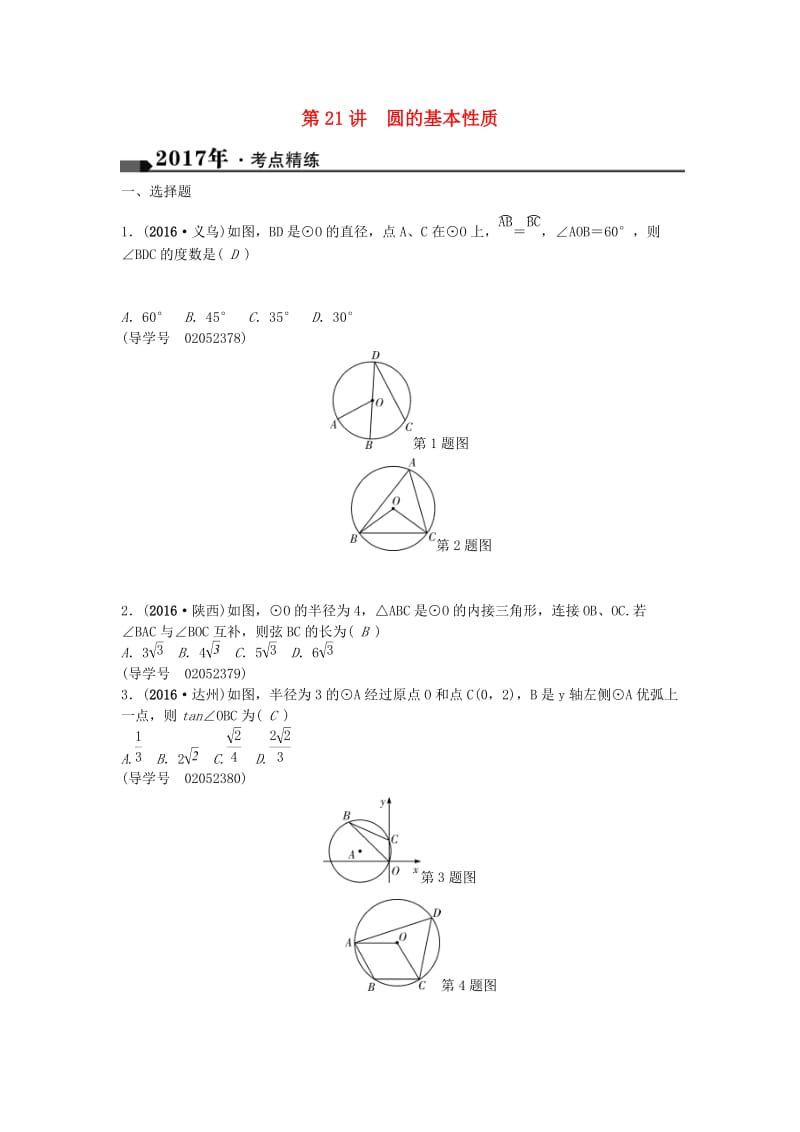
第21讲　圆的基本性质一、选择题1．(2016义乌)如图，BD是⊙O的直径，点A、C在⊙O上，＝，∠AOB＝60，则∠BDC的度数是( D )　　　　　　　　　　　　　　　　A．60 B．45 C．35 D．30(导学号　02052378)第1题图　　　第2题图2．(2016陕西)如图，⊙O的半径为4，△ABC是⊙O的内接三角形，连接OB、OC.若∠BAC与∠BOC互补，则弦BC的长为( B )A．3 B．4 C．5 D．6(导学号　02052379)3．(2016达州)如图，半径为3的⊙A经过原点O和点C(0，2)，B是y轴左侧⊙A优弧上一点，则tan∠OBC为( C )A. B．2 C. D.(导学号　02052380)第3题图　　　第4题图4．(2016兰州)如图，四边形ABCD内接于⊙O，若四边形ABCO是平行四边形，则∠ADC的大小为( C )A．45 B．50 C．60 D．75(导学号　02052381)5．(2016杭州)如图，已知AC是⊙O的直径，点B在圆周上(不与A、C重合)，点D在AC的延长线上，连接BD交⊙O于点E，若∠AOB＝3∠ADB，则( D )A．DE＝EB B.DE＝EBC.DE＝DO D．DE＝OB(导学号　02052382)第5题图　　　第6题图6．(2016安徽)如图，Rt△ABC中，AB⊥BC，AB＝6，BC＝4，P是△ABC内部的一个动点，且满足∠PAB＝∠PBC，则线段CP长的最小值为( B )A. B．2 C. D.(导学号　02052383)解析：∵∠ABC＝90，∴∠ABP＋∠PBC＝90，∵∠PAB＝∠PBC，∴∠BAP＋∠ABP＝90，∴∠APB＝90，∴点P在以AB为直径的⊙O上，如图，连接OC交⊙O于点P′，当P与P′重合时，此时PC最小，在Rt△BCO中，∵∠OBC＝90，BC＝4，OB＝3，∴OC＝＝5，∴PC＝OC－OP＝5－3＝2.∴PC最小值为2.故选B7．(2016丽水)如图，已知⊙O是等腰Rt△ABC的外接圆，点D是上一点，BD交AC于点E，若BC＝4，AD＝，则AE的长是( C )A．3 B．2 C．1 D．1.2(导学号　02052384) 二、填空题8．(2016巴中)如图，∠A是⊙O的圆周角，∠OBC＝55，则∠A＝__35__．(导学号　02052385)第8题图　　　第9题图9．(2016宿迁)如图，在△ABC中，已知∠ACB＝130，∠BAC＝20，BC＝2，以点C为圆心，CB为半径的圆交AB于点D，则BD的长为__2__．(导学号　02052386)10．(2016益阳)如图，四边形ABCD内接于⊙O，AB是直径，过C点的切线与AB的延长线交于P点，若∠P＝40，则∠D的度数为__115__．(导学号　02052387)第10题图　　　第11题图11．(2016枣庄)如图，在半径为3的⊙O中，直径AB与弦CD相交于点E，连接AC，BD，若AC＝2，则tanD＝__2__．(导学号　02052388)12.(2016山西百校联考二)如图，正方形ABCD内有一点O使得△OBC是等边三角形，连接OA并延长，交以O为圆心，OB长为半径的⊙O于点E，连接BD并延长交⊙O于点F，连接EF，则∠EFB的度数为__37.5__度．(导学号　02052389)13．(2016成都)如图，△ABC内接于⊙O，AH⊥BC于点H，若AC＝24，AH＝18，⊙O的半径OC＝13，则AB＝____．(导学号　02052390)解析：如图，作直径AE，连接CE，∴∠ACE＝90，∵AH⊥BC，∴∠AHB＝90，∴∠ACE＝∠AHB，∵∠B＝∠E，∴△ABH∽△AEC，∴＝，∴AB＝，∵AC＝24，AH＝18，AE＝2OC＝26，∴AB＝＝三、解答题14．(2016宁夏)已知△ABC，以AB为直径的⊙O分别交AC于D，BC于E，连接ED，若ED＝EC.(1)求证：AB＝AC；(2)若AB＝4，BC＝2，求CD的长．(导学号　02052391)(1)证明：∵ED＝EC，∴∠EDC＝∠C，根据圆内接四边形性质可得：∠B＋∠ADE＝∠ADE＋∠EDC＝180，∴∠EDC＝∠B，∴∠B＝∠C，∴AB＝AC(2)解：如图，连接AE，∵AB为直径，∴AE⊥BC，由(1)知AB＝AC，∴BE＝CE＝BC＝，在△ABC和△EDC中，∠C＝∠C，∠ABC＝∠EDC，∴△ABC∽△EDC，∴＝，即CECB＝CDCA，AC＝AB＝4，∴2＝4CD，∴CD＝15．(2016温州)如图，在△ABC中，∠C＝90，D是BC边上一点，以DB为直径的⊙O经过AB的中点E，交AD的延长线于点F，连接EF. (1)求证：∠1＝∠F；(2)若sinB＝，EF＝2，求CD的长．(导学号　02052392)(1)证明：如图，连接DE，∵BD是⊙O的直径，∴∠DEB＝90，∵E是AB的中点，∴DA＝DB，∴∠1＝∠B，∵∠B＝∠F，∴∠1＝∠F；(2)解：∵∠1＝∠F，∴AE＝EF＝2，∴AB＝2AE＝4，在Rt△ABC中，AC＝ABsinB＝4，∴BC＝＝＝8，设CD＝x，则AD＝BD＝8－x，∵AC2＋CD2＝AD2，即42＋x2＝(8－x)2，∴x＝3，即CD＝316.(2015烟台)如图，以△ABC的一边AB为直径的半圆与其他两边AC，BC的交点分别为D，E，且＝.(1)试判断△ABC的形状，并说明理由；(2)已知半圆的半径为5，BC＝12，求sin∠ABD的值．(导学号　02052393)解：(1)△ABC为等腰三角形．理由如下：连接AE，∵＝，∴∠DAE＝∠BAE，即AE平分∠BAC，∵AB为直径，∴∠AEB＝90，∴AE⊥BC，∴△ABC为等腰三角形；(2)∵△ABC为等腰三角形，AE⊥BC，∴BE＝CE＝BC＝12＝6，在Rt△ABE中，∵AB＝10，BE＝6，∴AE＝＝8，∵AB为直径，∴∠ADB＝90，∴AEBC＝BDAC，∴BD＝＝，在Rt△ABD中，∵AB＝10，BD＝，∴AD＝＝，∴sin∠ABD＝＝＝17．如图，已知⊙O的半径为1，A，P，B，C是⊙O上的四个点，∠APC＝∠CPB＝60 .(1)当点P位于的什么位置时，四边形APBC的面积最大？并求出最大面积； (2)试探究线段PA，PB，PC之间的数量关系，并证明你的结论．(导学号　02052394)解：(1)当点P为的中点时，四边形APBC的面积最大．如图①，过点P作PE⊥AB，垂足为E.过点C作CF⊥AB，垂足为F.∵S△APB＝ABPE，S△ABC＝ABCF，∴S四边形APBC＝AB(PE＋CF)，当点P为的中点时，PE＋CF＝PC，PC为⊙O的直径，∴此时四边形APBC的面积最大，∵∠APC＝∠ABC＝60，∠BPC＝∠BAC＝60，∴△ABC为正三角形，又∵⊙O的半径为1，∴其内接正三角形的边长AB＝，∴S四边形APBC＝2＝；(2)在PC上截取PD＝AP，如图②，又∵∠APC＝60，∴△APD是等边三角形，∴AD＝AP＝PD，∠ADP＝60，即∠ADC＝120.又∵∠APB＝∠APC＋∠BPC＝120，∴∠ADC＝∠APB，在△APB和△ADC中，，∴△APB≌△ADC(AAS)，∴BP＝CD，又∵PD＝AP，∴CP＝BP＋AP。