简单回归模型的基本假设

文档格式：PPT| 98 页|大小 2.05MB|积分 10|2023-02-06 发布|文档ID：185726767

下载文档

下载文档到电脑，查找使用更方便还剩页未读，继续阅读>>

侵权申诉举报

1 / 98

此文档下载收益归作者所有下载文档

版权提示

文本预览

常见问题

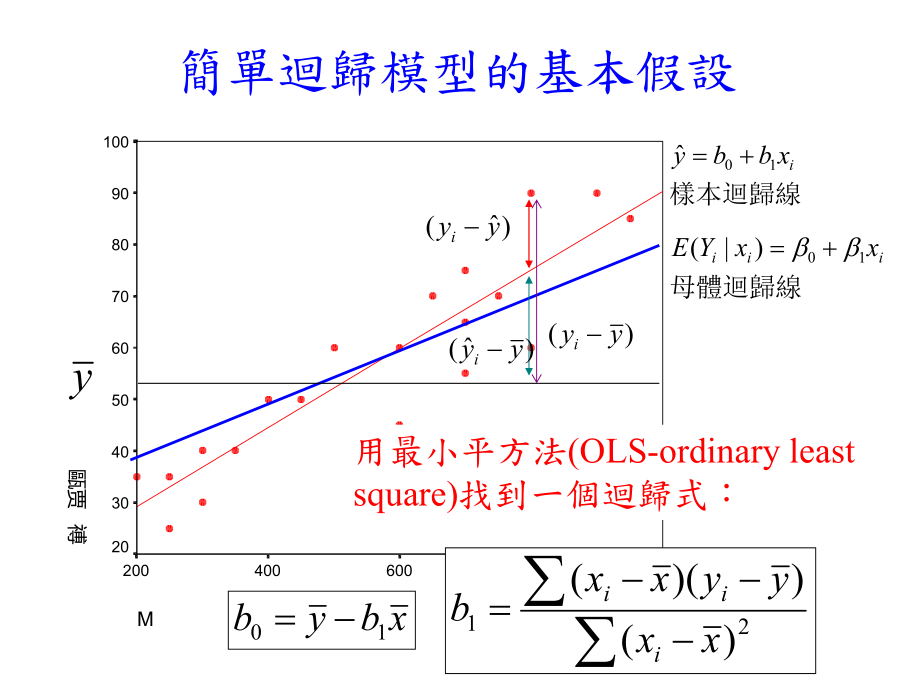
簡單迴歸模型的基本假設1000800600400200甌贾禣1009080706050403020樣本迴歸線ixbby10母體迴歸線iiixxYE10)|(y)(yyi)(yyi)(yyi21)()(xxyyxxbiiixbyb10用最小平方法(OLS-ordinary least square)找到一個迴歸式：YxiF(Y)XXYE10)|(1x2xnx0iiixxyE)(Population regression line我們假設在母體中，對於每一個xi值而言，其相對應的yi值遵循某種機率分配，且期望值為與x相對應的一組y，其期望值剛好落在一條直線上我們假設這些分配有相同的變異數2Page 3我們對於上面的迴歸模型有以下的假設（限制）：linearity依變項Yi與自變項之間的關係為線性：Normality:ei為常態分配(或依變數為一常態分配）eiN or YiNZero conditional mean:對於每個xi，E(ei|Xi)=0 殘差項的平均數為零 Independence of ei and Xi:殘差值與Xi不相關Cov(ei,X)=0 or E(ei,X)=0 簡單迴歸模型的基本假設iiieXbbY10Page 4簡單迴歸模型的基本假設Homoscedasticity:Var(ei)=2變異數齊一性每組的殘差項的變異數均相等。

而每一組的變異數實際上是指X=xi條件下的Y之變異數，因此2也可以表為2Y|X綜合以上：eiN(0,2)YiN(b0+b1Xi,2)No serial correlation:ei彼此不相關 Cov(ei,ej)=0X為一固定變數或事前決定之變數，Y為一隨機變數Page 5簡單迴歸模型的基本假設 linearity:假設依變項Yi與自變項之間的關係為線性：iiiexbbY10我們假設隨機誤差項ei有下列的性質：Normality:ei為常態分配Zero conditional mean:對於每個xi，E(ei|xi)=0 Independence of ei and xi:殘差值與xi不相關Homoscedasticity:Var(ei)=2No serial correlation:ei彼此不相關Page 6Residuals Sum to Zero 0ieiiiyye)(10iixbbyiixbnby10兩邊除以n0110bxbynxbbnyneiii0b0)(neeEiiPage 7YXF(Y)XXYE10)|(1x2xnx0E(e|xi)=0given X,the mean of the distribution of “other factors”is zero無論xi為什麼數值，ei的平均值皆為0其他因素與X無關Page 8殘差值與xi不相關0),(iixeCov)()(),(iiiiiixExeEeExeCov)(iiixExeE0)(iiiixEexeE)()(iiiixEeExeE0),(iixe證明Cov0 等於證明iixeE0 等於證明nxexeEiiiiPage 9殘差值與xi不相關 0證明iiexiiiiexxex)(iiiiiexexexx)()(10iiixbbyxx0 0iiex)(11iiixbxbyyxxxbyb1021)()(xxbyyxxiii22)()()()(xxxxyyxxyyxxiiiiii)(iiiyyxxiixbby10Page 10No serial correlation:ei彼此不相關ji,eCov(eji,0)0)()()()jijjiijieeEeEeeEeE,eCov(e兩個殘差值不相關表示它們彼此之間為獨立(independent)，由於我們抽取的是隨機樣本，因此每一個觀察值之間彼此沒有關連。

也就是說，某一戶人家的娛樂支出不會影響另一戶人家的育樂支出0)()()()jijjiijieeEyEyyEyE,yCov(y1nyyxxsiiXYPage 11YXF(Y)XBBXYE10)|(1x2xnx0Estimation of e2前面我們假設Homoscedasticity:Var(ei)=2每一個相對應於x值的y不但為常態分配，且有相同的變異數222(Xi,Yi)are independently and identically distributedYxiF(Y)XBBXYE10)|(1x2xnx0iiixxyE)(Population regression line我們假設在母體中，對於每一個xi值而言，其相對應的yi值遵循某種機率分配，且期望值為YXF(Y)XBBXYE10)|(1x2xnx0Sample regression line從樣本中可以推估出0,1的估計值，也可以建構出樣本迴歸線由於母體參數0,1為未知數，因此母體迴歸線必須透過觀察到的樣本(xi,yi)來推估iixbby10由於觀察到樣本點(xi,yi)不會剛好落在母體迴歸線上，因此yi與E(yi|xi)會有所差距。

Page 14區分母體與樣本迴歸線由於我們是從樣本中來估計迴歸線，用來估計迴歸線的截距b0及斜率b1 的估計式(estimator)為具有抽樣分配(sampling distribution)的隨機變數觀念iiixBBy10iiiexbby10母體迴歸線樣本迴歸線Page 15截距與斜率的抽樣分配我們想進一步知道從樣本中估計的截距b0及斜率b1 是不是能夠正確的反映出母體的參數B0及B1雖然每一次從樣本中估計出來的迴歸線都不同，但我們如果我們知道估計式的抽樣分配，則可以用統計檢定的方式來對我們的樣本參數進行統計的推估因此我們第一步需要知道為截距b0及斜率b1 的抽樣分配為何？也就是說他們的期望值及標準差為何？觀念Page 16迴歸的統計檢定統計檢定包含兩部分:(1)對截距與斜率的檢定(2)迴歸方程式的配適度區分母體與樣本迴歸線1000800600400200甌贾禣1009080706050403020樣本迴歸線ixbby10母體迴歸線iiixxyE10)|(迴歸預測值的差距實際值與母體i本迴歸線的差距實際值與樣ieixbby10iixyE10)(iyPage 18區分母體與樣本迴歸線因此每一個實際的觀察值可以表為母體迴歸線的函數或是樣本迴歸線的函數)|(iiiixyEy iiiyyeiiixxyE10)|(ixbby10iiixy10iiexbb10 我們經常用可觀察的殘差值ei(residual)來推估未知的iPage 19截距與斜率的抽樣分配其中截距0及斜率1 為參數，xi為已知常數，且觀念iiixy10),0(2Ni 由於yi為常態分配的線性組合(i為常態分配)，故yi亦為一常態分配Page 20斜率b1的抽樣分配 b1分配的型態為何？E(b1)=?Var(b1)=?觀念21)()(xxyyxxbiii2)()()(xxyxxyxxiiii2)()()(xxxxyyxxiiii=0iiiyxxxx)()(2由於xi為已知常數，因此b1的分配為常態分配yi的線性組合，故b1為常態分配Page 21斜率b1的抽樣分配 E(b1)=?觀念iiiyxxxxb21)()(iiixy10210)()(xxxxxiiii22120)()()()()()(xxxxxxxxxxxxxiiiiiiiiPage 22斜率b1的抽樣分配觀念221201)()()()()()(xxxxxxxxxxxxxbiiiiiiii樣本觀察值與平均數之差的總合為零xxxxxxxxxxSiiiiixx)()()()()(xxxxxxiiiiixxx)(211)()(xxxxbiiiPage 23斜率b1的抽樣分配觀念)()()(211xxxxEbEiii為已知常數及因為xxi)()()()(211iiiExxxxbE等於零11)(bEb1為1的不偏估計式unbiased estimatorPage 24斜率b1的抽樣分配觀念)()()(21xxyxxVarbVariii為已知常數及因為xxi)var()()()(2221iiiyxxxxbVar)var()var(2yccy 利用21)(var)var(iiioiVarxy常數),0(2NixxxxixxiSSSSSSybVar21)var()var()(Page 25斜率b1的抽樣分配觀念2112111)()()(bEbEbEbVar11)(bE211)()(xxxxbiii22211)()()(xxxxEbEiii222)()(1iiixxExx)(2)()()()(12121222222212122xxxxxxxxxxExxnniPage 26斜率b1的抽樣分配觀念)(2)()()()(12121222222212122xxxxxxxxxxExxnni00)()()()(12222222122xxxxxxxxni222)()()var(iiiiEEEjiEji,0)(2222)()(xxxxii22)(xxixxSSbVar21)(Page 27斜率b1的抽樣分配觀念從以上的討論得知：),(211xxSSNb)(,(22200 xxnxNbiib0的抽樣分配證明略)1,0()(2211NxxbZi未知數Page 28Estimation of e2 令真正的變異數(true variance)可分別表為2b0及2b1。

一般而言，2b0及2b1通常為未知數(因為2未知)，必須從樣本中估計求得，以符號S2b0及S2b1來表示估計的變異數同理，我們以b0及b1來表示b0及b1的真正標準誤差，以Sb0及Sb1來表示估計的標準誤差(estimated standard error)觀念Page 29Estimation of e2222)()()var(iiiieEeEeEe222)()()var(iiiieEyEyEy如何估計2?一個簡單的方法為利用Sum of Square Error(SSE)來估算222212nieeeEeE22221neEeEeE2222n22neEiPage 30Estimation of e2但實際上，因為我們不知道真正的母體迴歸線，所以也就無法知道真正的殘差值ei（更正式的寫法為i)因此我們必須以估計的殘差值來取代)(10iiiiixbbyyye22neEi但222neEiPage 31Estimation of e2在迴歸式中，SSE的自由度為樣本個數減去估計係數的數目)1(2KnSSESeSe為迴歸線的估計標準差(estimated standard error of the regression)，代表每一個相對應於x值的Y，分佈於迴歸線上的變異狀況。

Se愈小，表示Y的散佈愈集中Page 32Estimation of e2)1(2KnSSESe在簡單迴歸中：2)(2222nyynenSSESiiie2102nyxbybySiiiiePage 33Estimation of e2iiiiyxbybySSE102證明iiieeeSSE2)(iiiyyeiiiieyyeiiiiexbbye)(10iiioiiexbebye1iiiyxbby)(10iiiiyxbyby102=0Page 34Estimation of e2222)()(1xxbyySSEii證明21022)()(iiiixbbyyyeSSExbyb10211)(iixbxbyy21)()(xxbyyii)(2)()(12212yyxxbxxbyyiiii2112212)(2)()(xxbbxxbyyiii222)()(1xxbyyiixxyySSbSSSSE2121)()(xxyyxxbiiiPage 35Estimation of e2222)()(1xxbyySSEii2212)()()()(xxxxyyxxbyyiiiii)()(12yyxxbyyiiixyyySSbSSSSE1xxxyyyiiSSSSSSyySSE22)()(xxxySSSSb 1Page 36公式整理nyyynyyySSiiiiyy22222)()(nxxxnxxxSSiiiixx22222)()(yxnyxyyxxSSiiiixy)(xxxySSSSb 1nyxyxiiii)(xxxyyyiiSSSSSSyySSE22)()(xxyyxyyySSbSSSSbSSSSE211Page 37Estimation of e2stock股利xi股價yi預測價格eiei2113115112.79532.20474.8607244545.2305-0.23050.05313312100105.2881-5.288127.964455052.7377-2.73777.495565560.2449-5.244927.509688575.25939.740794.8812734037.72332.27675.18336845045.23054.769522.7481954552.7377-7.737759.8721077067.75212.24795.05305654.99940.0006255.6222neSieiixy5072.72017.15952.312106196.255eSPage 38Estimation of e2stock股利xi股價yixi*yixi2yi211311514951691322524451801620253121001200144100004550250252500565533036302568856806472257340120916008450200162500954522525202510770490494900sum67655517055349025iiiiyxbybySSE102663.255)5170)(5072.7()655)(2017.15(49025SSEiixy5072.72017.15Page 39Estimating standard error of b0 and b1 觀念截距b0及斜率b1的變異數的公式niiniiniiniibxxnxxnxnxbVar1212212212220)()(0niiniibxxxnxbVar1221222211)(Page 40Estimating standard error of b0 and b1觀念由於2未知2221xxsxnxssieieb222220 xxnsxnxnxssixeiiebiEstimated standard error of b1Estimated standard error of b02)(2222nyynenSSESiiiePage 41Hypothesis Testing in the Linear Regression Model觀念若以S2e來推估2，則)1,0()(2211NxxbZi)2()(2211ntxxSbtie 知道b1的分配及標準誤差後，我們可以進行統計推論Page 42Hypothesis Testing in the Linear Regression Model觀念在迴歸的統計檢定中，我們想要知道自變數x是否對於解釋y有用，也就是說x與y之間是否具有線性關係？iiixxyE10)|(一般而言，如果x與y之間存在一線性關係，則10Page 43Hypothesis Testing in the Linear Regression Model觀念我們要檢驗下列的虛擬假設：0:10H0:11H0:11H0:11H0:10H0:10HOne-side test 學歷與薪資的關係One-side test 私校學費與註冊人數之關係Two-side test 父母的收入與兒女的在校成績0:or 10H0:or 10HPage 44Hypothesis Testing in the Linear Regression Model觀念我們也可以檢驗斜率等於某特定值*：2000:10H2000:11H每增加一年的學歷薪水增加$2000Page 45Hypothesis Testing in the Linear Regression Model觀念斜率的單邊假設檢定：*111:H*110:H*110:or H1*11bSbt02,Hrejectttn則如果)tP(t valuecritical2-n .2,使分配中的為在ttnPage 46Hypothesis Testing in the Linear Regression Model觀念斜率的單邊假設檢定：*111:H*110:H*110:or H1*11bSbt02,Hrejectttn則如果)-tP(t valuecritical2-n .2,使分配中的為在ttnPage 47Hypothesis Testing in the Linear Regression Model觀念斜率的雙邊假設檢定：*111:H*110:H1*11bSbt02,2 Hrejectttn則如果02,2 Hrejectttn則如果Page 48例題上例收入與支出的關係，以=.01檢定H0:1=0 vs.1 0 (.054)(18.82)9733.R 92.016.82ixyexpenditureincome200250300350400200300400896.210.17054.9232.08,01.11tSbtb896.28,01.tPage 49例題上例收入與支出的關係，以=.05檢定H0:1=.90 vs.1.90 (.054)(18.82)9733.R 9232.016.82ixy306.24298.054.90.9232.8,025.*111tSbtb306.28,025.tPage 50截距的檢定例題續上例，以=.05檢定H0:0=0 vs.0 0 (.054)(18.82)9733.R 9232.016.82ixy306.2433.82.180162.808,025.00tSbtb306.28,025.t306.28,025.tPage 51Confidence Intervals for the Regression Coefficientst依循自由度為(n-2)的t分配:111bsbt1,2,2vvtttP1,211,21vbvtsbtP111,211,21bvbvstbstbPPage 52Confidence Intervals for the Regression Coefficients上述公式指出，如果我們重複抽樣來計算樣本迴歸線的斜率，則1的值有100(1-)%的機率會落於以下區間：11,21,21 ,bvbvstbstb111,211,21bvbvstbstbP其中t值得自當自由度為=(n-2)時的t分配,上述的區間稱為1的100(1-)%信賴區間。

同理，我們可以找出截距的信賴區間：00,20,20,bvbvstbstbPage 53例題求下列迴歸線斜率的90%信賴區間，(n=10):(.054)(18.82)9733.R 9232.016.82ixy11,21,21,bvbvstbstb)02365.1 ,82277.0(054.860.19232.0 ,054.860.19232.0860.1,8)2(,05.08,05.tnvPage 54迴歸方程式的解釋力當我們計算出迴歸線後，我們想進一步知道迴歸曲線與資料間的適合度(goodness of fit)母體迴歸線告訴我們x與y有下列線性關係iiiexbbY10 上式告訴我們有兩個因素會影響Y值的變異：Y值會隨著xi值的改變而變：這一部份的變異為被迴歸線解釋的變異Y值會隨著ei值而變：這一部份為迴歸線無法解釋的變異Page 55簡單迴歸模型1000800600400200甌贾禣1009080706050403020迴歸線ixbby10y)(yyi)(yyi)(yyi被解釋的變異未被解釋的變異)()()(yyyyyyiiii總變異量沒有解釋能力的回歸線Page 56iiiyyeiiieyy iiieyyyy變異數的分解未被解釋的變異稱為殘差值residual，第i個觀察值的殘差值定義為:y 兩邊減取平方和22iiieyyyy)()()(iiiiyyyyyy改寫成或將)(yyiPage 57變異數的分解22iiieyyyy222iiiieyyeyyiiiieyyeyy222iiiiieyyeeyyiiieyxbbe)(10iiiieyexbbe)(10010iiiieyexbebPage 58變異數的分解222iiieyyyySSESSRSST 總變異量Sum of Square Total解釋變異量Regression Sum of Square 未解釋變異量Sum of Square ErrorPage 59變異數的分解SSESSRSSTSSESSTSSRSSTSSESSTSSR 1SSTSSESSTSSRR12102 R兩邊除SSTR2愈大，表示X對Y的解釋能力愈強判定係數為可解釋變異量佔總變異量的比例，表示X對Y的變異之解釋能力。

Page 60yyniiSSyySST122212112)(xxbSSbSSESSTyySSRixxniixxyyniiSSbSSeSSE2112變異數的分解Page 61yySSRSSE)1(2變異數的分解SSTSSESSTSSRR12SSTRSSE)1(2yyxxSSSSbSSTSSRR212xxSSbSSR21YXssbr1Page 6211)(2222nxnxnxxSiix11)(2222nynynyySiiy22212yxssbR 變異數的分解以樣本變異數來計算0 022yxSS0 ifonly and if,012bRPage 63stock股利xi股價yixi*yixi2yi211311514951691322524451801620253121001200144100004550250252500565533036302568856806472257340120916008450200162500954522525202510770490494900sum67655517055349025iixy5072.72017.155.122,6)5.65(10025,492222ynyyySSTiiiiiiyxbybySSE102663.255)5170)(5072.7()655)(2017.15(49025SSE9582.5.122,66196.255112SSTSSER求R2?Page 64567.119)7.6(1055312222nxnxSix278.6809)5.65(10025,4912222nynySiy9582.278.680567.115072.7222212yxssbRstock股利xi股價yixi*yixi2yi211311514951691322524451801620253121001200144100004550250252500565533036302568856806472257340120916008450200162500954522525202510770490494900sum67655517055349025Page 65F-檢定變異來源平方和(SS)自由度(d.f)平均平方和(M S)F迴歸SSR1M SR=SSR/1F=M SR/M SE誤差SSEn-2M SE=SSE/(n-2)總和SSTn-1F檢定統計量可檢定下列假設:H0:迴歸方程式無解釋能力(1=0)H1:迴歸方程式有解釋能力(1 0)Page 66Page 67r=0.994 r2=0.989Page 68r=0.921 r2=0.849Page 69Page 136)635.0(93.64ageheightPage 70r2Variance of value y=5.30091Variance of predicted y=5.241359888.030091.524135.5 y valueobserved of variance valuepredicted of iancevar2yrPage 71Page 72例題求迴歸線yi=b0+b1xi+ei 的斜率與截距並計算R2及兩個係數的估計標準誤差。

x y xyx2y240035014000016000012250030025075000900006250035032511375012250010562540037014800016000013690020018036000400003240030027081000900007290037533012375014062510890038035013300014440012250032530097500105625900004003601440001600001296003430 3085 1092000 121315098382534310/3430 x5.30810/3085y2211010 xxyxyxbiiiii9232.)343(103430)5.308)(343(1010920002162.810 xbybPage 73例題畫出迴歸線：ixy92.016.8expenditureincome200250300350400200300400Page 74例題50.102,3210210121012yyyySSTiiii367.856102iiiiyxbybySSE046.10722nSSEse346.10es9733.12SSTSSERPage 75例題x y xyx2y23430 3085 1092000 1213150983825054.)343(101213150346.102221xnxssieb346.10es8211.18)343(101213150101213150346.1022220 xnxnxssiiebPage 76例題 1987年USA Today報導一研究發現懷孕時吸煙的母親，其兒女在三歲時的IQ比不吸煙的母親平均少5分，你想驗證上述的假設，記錄母親懷孕時每日的吸煙根數(xi)及兒女在三歲時的IQ(yi)，你心中假設的模型為：iiixxYE10)|(抽取父母親IQ相當的20個樣本家庭，計算樣本迴歸模型如下：8.7S (.15)(1.2)17.R 60.104e2iixy請分析這個結果Page 77例題8.7S (.15)(1.2)17.R 60.104e2iixy斜率為-0.60如何解釋？代表樣本中，母親每吸一根菸，baby的智商減少0.60分截距為104如何解釋？代表不吸煙母親的子女的智商預測值為104Page 78例題8.7S (.15)(1.2)17.R 60.104e2iixy可不可以將樣本所得的結果推論至母體(概化)？必須檢定母親的吸煙對兒女智商無影響的假設，即0:10H0:H100.415.60.11bSbt734.118,05.t0:Rejected10HPage 79例題8.7S (.15)(1.2)17.R 60.104e2iixyThe 95%confidence interval:11,21,21,bvbvstbstb15.101.260.,15.101.260.)2849.,9152.(表示在95%的信心水準下，我們可以說真正的1值介於此區間中。

Page 80例題8.7S (.15)(1.2)17.R 60.104e2iixy R2=0.17 說明母親的吸煙數量解釋了17%的兒女IQ變異量或者說，尚有83%的IQ變異無法由抽煙與否來解釋Page 81Prediction using the regression model 迴歸線可以用來估計在某一特定x值之下，Y的預測值：我們可以用迴歸線來估計在xi下的”新”觀察值YiiixY 我們也可以用迴歸線來估計在xi下的Y的期望值iiixxYE)|(Page 82Prediction using the regression model 由於我們不知道母體迴歸線，因此Yi及E(Y|xi)最好的預測值為雖然特定Yi的預測值與預測的期望值E(Yi|xi)相同，皆為b0+b1xi但兩者的抽樣誤差不同，因為估計Yi的期望值不需要考慮隨機誤差項eiiixbby1Page 83Prediction using the regression model Effects of Sampling Error:預測Yi的期望值E(Yi|xi)會有來自於用樣本迴歸線來估計母體迴歸線所造成的抽樣誤差iixbby1)|(iixYEy不會剛好等於iiixxYE)|(估計Page 84Prediction using the regression model Effects of Sampling Error:預測單獨Yi的值會有來自於用樣本迴歸線來估計母體迴歸線所造成的抽樣誤差+用0來推估i 的誤差。

01iixbbyiYy不會剛好等於估計iiixYYXF(Y)XBBXYE10)|(1x2xnx0Confidence Interval for Predictions我們希望知道樣本迴歸線的預測值(y-hat)的抽樣分配，才能對E(Y|xi)從事統計推論iixbby10區分母體與樣本迴歸線1000800600400200甌贾禣1009080706050403020樣本迴歸線ixbby10母體迴歸線iiixxyE10)|(|iiiixYEy iiiyyeixbby10iixyE10)(iy特定)|(iixYEy Page 87E(Y|xi)之估計與檢定=某特定值xp時，Yp的期望值?ppxbby10)()|(10pppxbbExyE)()(10bExbEppxBB10Page 88E(Y|xi)之估計與檢定=某特定值xp時，Yp的變異數=?ppxbby10pxbxby11)(1xxbyp)()(10ppxbbVaryVar)(1xxbyVarp)()(12bVarxxnyVarpi2222)()(xxxxniepe)()(1222xxxxnipePage 89E(Y|xi)之估計與檢定)()(1222xxxxnipe,(10pxBB 因此E(Yp|xp)的抽樣分配為NxYEpp)|(以se來取代e)()(1222xxxxnsipe,(10pxBB NxYEpp)|(Page 90E(Y|xi)之估計與檢定在一特定xp值下，其相對應的期望值E(Yp|xp)的(1-)的信賴區間為222,2)(1xnxxxnstYpevpPage 91E(Y|xi)之估計與檢定在一特定xp值下，其相對應的預測值Yp的(1-)的信賴區間為222,2)(11xnxxxnstYpevp)|(的信區間較pppxYEYPage 92E(Y|xi)之估計與檢定其他條件不變，樣本數n愈大，預測值的信賴區間愈小，我們對預測的信心隨著樣本數的增加而增加。

222,2)(1xnxxxnstYpevpPage 93E(Y|xi)之估計與檢定其他條件不變，se愈大，預測值的信賴區間愈大Se為e的估計，代表依變項觀察值Yi與及其期望值之間的差異，se愈大，表示Yi愈不集中於母體迴歸線的週遭222,2)(1xnxxxnstYpevpPage 94E(Y|xi)之估計與檢定其他條件不變，sx2 愈大，我們對x值的分佈知道的愈廣，因而對Y的預測會愈準222,2)(1xnxxxnstYpevp222)1()(xisnxxxnxiPage 95E(Y|xi)之估計與檢定特定的xp值離x分佈的中心值愈遠，則我們的預測越不準CI最窄的部分出現在222,2)(1xnxxxnstYpevp222)1()(xisnxxxnxixxpPage 96例題汽車保養費Yi與車齡xi呈線性關係，取15輛車來估計迴歸線得iixy255050)(,50,302xnxxse假設求當xp=1,2,3,49時，Yi期望值得95%信賴區間Page 97例題iixy255050)(,50,302xnxxse假設160.2 13)2(,05.013,025.tnvPage 98例題特定的xp值離x分佈的中心值愈遠，則我們的預測越不準。

CI最窄的部分出現在x-bar。

点击阅读更多内容