人教版 小学9年级 数学上册 第二十四章圆24.3正多边形和圆拓展提高同步检测含解析

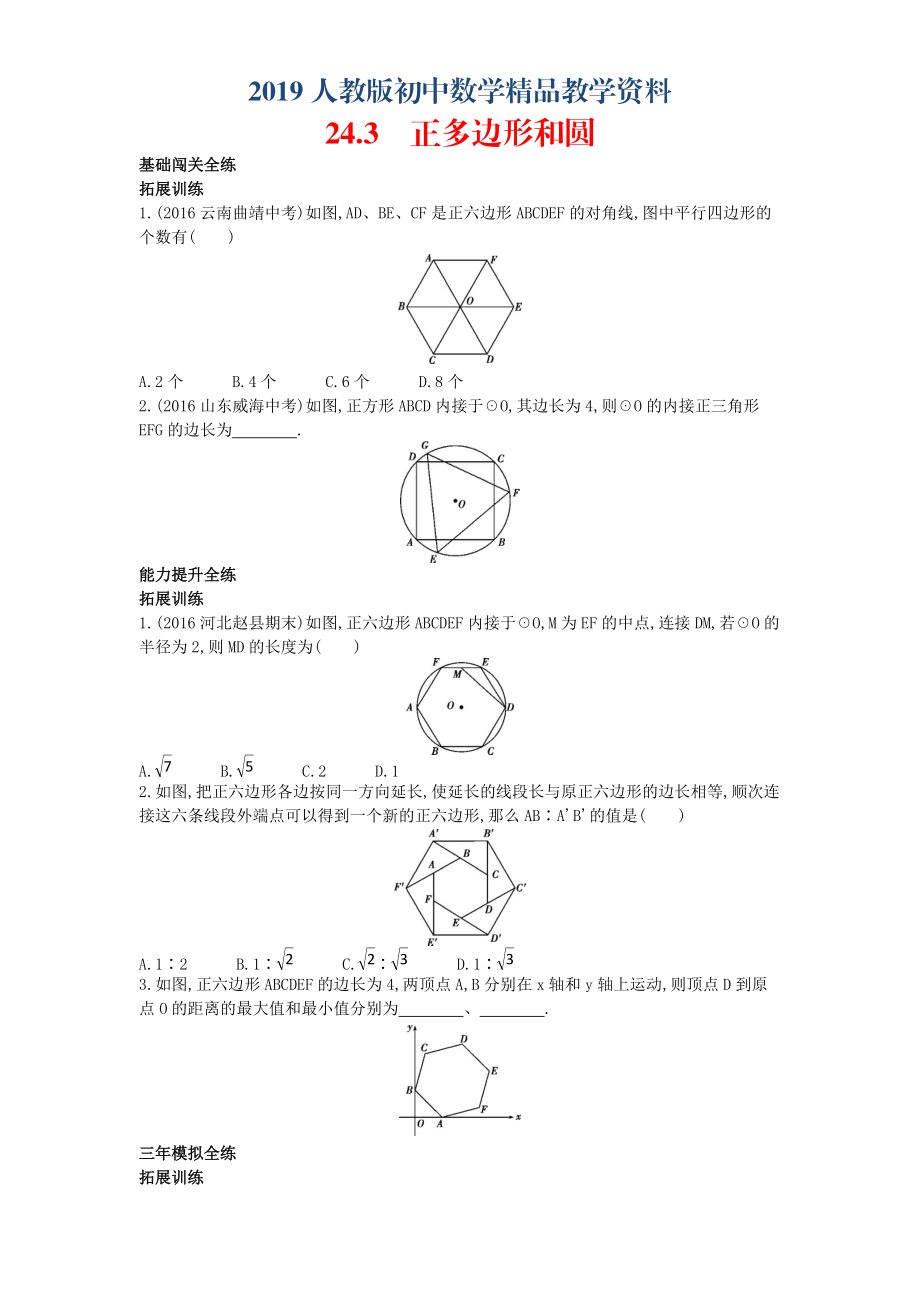
2019人教版初中数学精品教学资料24.3　正多边形和圆基础闯关全练拓展训练1.(2016云南曲靖中考)如图,AD、BE、CF是正六边形ABCDEF的对角线,图中平行四边形的个数有(　　)A.2个　　　B.4个　　　C.6个　　　D.8个2.(2016山东威海中考)如图,正方形ABCD内接于☉O,其边长为4,则☉O的内接正三角形EFG的边长为　　　　.能力提升全练拓展训练1.(2016河北赵县期末)如图,正六边形ABCDEF内接于☉O,M为EF的中点,连接DM,若☉O的半径为2,则MD的长度为(　　)A.7　　　B.5　　　C.2　　　D.12.如图,把正六边形各边按同一方向延长,使延长的线段长与原正六边形的边长相等,顺次连接这六条线段外端点可以得到一个新的正六边形,那么AB∶AB的值是(　　)A.1∶2　　　B.1∶2　　　C.2∶3　　　D.1∶33.如图,正六边形ABCDEF的边长为4,两顶点A,B分别在x轴和y轴上运动,则顶点D到原点O的距离的最大值和最小值分别为　　　　、　　　　.三年模拟全练拓展训练1.(2017湖北武汉江汉月考,15,★★☆)如图,为了拧开一个边长为a的正六边形螺帽,扳手张开b=30 mm时正好把螺帽嵌进,则螺帽的边长a为　　　　mm.2.(2016江西模拟,9,★★☆)如图,等边三角形ABC内接于半径为1的☉O,以BC为一边作☉O的内接矩形BCDE,则矩形BCDE的面积为　　　　.五年中考全练拓展训练1.(2016四川泸州中考,10,★★☆)以半径为1的圆的内接正三角形、正方形、正六边形的边心距为三边作三角形,则该三角形的面积是(　　)A.38　　　B.34　　　C.24　　　D.282.(2017浙江台州中考,16,★★☆) 如图,有一个边长不定的正方形ABCD,它的两个相对的顶点A,C分别在边长为1的正六边形一组平行的对边上,另外两个顶点B,D在正六边形内部(包括边界),则正方形边长a的取值范围是　　　　.核心素养全练拓展训练1.(2014湖南常德中考)阅读理解:如图①,在平面内选一定点O,引一条有方向的射线Ox,再选定一个单位长度,那么平面上任一点M的位置可由∠MOx的度数θ与OM的长度m确定,有序数对(θ,m)称为M点的“极坐标”,这样建立的坐标系称为“极坐标系”.应用:在图②的极坐标系下,如果正六边形的边长为2,有一边OA在射线Ox上,则正六边形的顶点C的极坐标应记为(　　)A.(60,4)　　B.(45,4) C.(60,22)　　D.(50,22)2.(2017北京昌平期末)如图,点A,B,C,D,E为☉O的五等分点,动点M从圆心O出发,沿线段OA→劣弧AC→线段CO的路线做匀速运动,设运动的时间为t,∠DME的度数为y,则下列图象中表示y与t之间函数关系最恰当的是(　　)24.3　正多边形和圆基础闯关全练拓展训练1.答案　C　∵六边形ABCDEF是正六边形,∴△OAB和△AOF都是正三角形,∴∠BAO=∠OAF=∠AFO=60,∴∠BAF+∠AFO=180,∴AB∥CF.同理,CF∥DE,∴AB∥CF∥DE.同理,AF∥BE∥CD,BC∥AD∥EF.∴四边形ABOF、FAOE、EFOD、CDEO、BCDO、ABCO均为平行四边形.故选C.2.答案　26解析　连接AC、OE、OF,作OM⊥EF于M,∵四边形ABCD是内接于☉O的正方形,∴AC是☉O的直径,AB=BC=4,∠ABC=90,∴AC=42,∴OE=OF=22,∵OM⊥EF,∴EM=MF,∵△EFG是内接于☉O的等边三角形,∴∠G=60,∴∠EOF=120,∴∠OEM=30.在Rt△OME中,∵OE=22,∠OEM=30,∴OM=2,EM=6,∴EF=26.∴☉O的内接正三角形EFG的边长为26.能力提升全练拓展训练1.答案　A　如图,连接OM、OD、OF,∵正六边形ABCDEF内接于☉O,M为EF的中点,∴OM⊥OD,OM⊥EF,∠MFO=60,∴∠MOD=∠OMF=90,在Rt△OMF中,由勾股定理可得OM=3,∴MD=OM2+OD2=(3)2+22=7.故选A.2.答案　D　∵六边形ABCDEF是正六边形,∴∠ACB=60,设AB=BC=a,又延长的线段长与原正六边形的边长相等,所以AC=2a,易知∠ABC=90,所以BC=a,由勾股定理可得AB=(2a)2-a2=3a,∴AB∶AB=a∶3a=1∶3.故选D.3.答案　2+213;213-2解析　当O、D、AB中点共线时,OD有最大值和最小值,如图,易知BD=43,BK=2,∠DBA=90,∴DK=BD2+BK2=52=213,∵K为AB中点,∠AOB=90,∴OK=BK=2,∴OD的最大值为2+213,同理,当O、D、AB中点共线时,将正六边形绕AB中点K旋转180,此时OD取得最小值,为213-2.三年模拟全练拓展训练1.答案　103解析　设正多边形ABCDEF的中心是O,∴∠AOB=∠BOC=60,∴OA=OB=AB=OC=BC,∴四边形ABCO是菱形,∴AC⊥OB,∠BAM=30,∴AB=2BM,AM=CM=15.在Rt△ABM中,BM2+AM2=AB2,即BM2+152=(2BM)2,解得BM=53(舍负),∴a=AB=2BM=103(mm).2.答案　3解析　如图,连接BD.∵△ABC是等边三角形,∴∠BAC=60,∴∠BDC=∠BAC=60.∵四边形BCDE是内接于☉O的矩形,∴∠BCD=90,BD是☉O的直径,∴∠CBD=90-60=30,BD=2,∴CD=1,∴BC=BD2-CD2=3,∴S矩形BCDE=BCCD=31=3.五年中考全练拓展训练1.答案　D　如图①,连接OB,过O作OD⊥BC于D,则∠OBC=30,OB=1,∴OD=12;如图②,连接OB、OC,过O作OE⊥BC于E,则△OBE是等腰直角三角形,则2OE2=OB2,即OE=22R=22;如图③,连接OA、OB,过O作OG⊥AB于G,则△OAB是等边三角形,故AG=12,∴OG=32,故圆内接正三角形、正方形、正六边形的边心距分别为12、22、32,又因为122+222=34,322=34,所以该三角形是直角三角形,所以该三角形的面积为121222=28,故选D.2.答案　62≤a≤3-3解析　如图①,根据题意,AC为正方形对角线,则当A、C分别是正六边形平行的两边中点时,此时AC最短,正方形边长也最短,易求得AC=3,∴边长最小为62.当正方形四点都在正六边形上时,如图②,则OQ⊥FP,∠FOP=45,∠FQP=60,设FP=x,则OP=x,PQ=33x,∴OQ=x+33x=1,∴x=3-32,此时边长取得最大值,为3-3.∴正方形边长a的取值范围是62≤a≤3-3.图①图②核心素养全练拓展训练1.答案　A　如图,设正六边形的中心为D,连接AD,∵∠ADO=3606=60,OD=AD,∴△AOD是等边三角形,∴OD=OA=2,∠AOD=60,∴OC=2OD=22=4,∴正六边形的顶点C的极坐标应记为(60,4).故选A.2.答案　B　当点M与点O重合时,∠DME为圆心角,∠DME=3605=72;当点M在OA上运动时,∠DME为圆内角,且逐渐变小;当点M在劣弧AC上运动时,∠DME为圆周角,始终不变,∠DME=12∠DOE=36;当点M在OC上运动时,∠DME为圆内角,且逐渐变大.根据上述描述,可知函数图象为选项B中图象,故选B.。